Funciones Trigonometricas
Historia
El estudio de las funciones trigonométricas se remonta a la época de babilonia, y gran parte de los fundamentos de trigonometria fueron desarrollados por los matemáticos de la Antigua Grecia, de la India y estudiosos musulmanes.
El primer uso de la función seno (sin(·)) aparece en el Sulba Sutras escrito en India del siglo VIII al VI a. C. Las funciones trigonométricas fueron estudiadas por Hiparco de Nircea (180-125 a. C.), Aryhabatha (476-550), Varahamihira, Brahmagupta, Al-Khwarizimi, Abu'l-Wafa,Omar Khayyam, Bhaskara II, Nasir al-Din Tusi, Regiomontanus (1464), Ghiyath al-Kashi y Ulugh Beg (Siglo XIV), Madhawa (ca. 1400), Rheticus, y el alumno de éste, Valentin Otho. La obra de Leonhard Euler Introductio in analysin infinitorum (1748) fue la que estableció el tratamiento analítico de las funciones trigonométricas en Europa, definiéndolas como series infinitas presentadas en las llamadas "Fórmulas de Euler".
La noción de que debería existir alguna correspondencia estándar entre la longitud de los lados de un triángulo siguió a la idea de que triángulos similares mantienen la misma proporción entre sus lados. Esto es, que para cualquier triángulo semejante, la relación entre la hipotenusa y otro de sus lados es constante. Si la hipotenusa es el doble de larga, así serán los catetos. Justamente estas proporciones son las que expresan las funciones trigonométricas.
Integral de la Primera y Segunda función Trigonométrica
Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triangulo rectangulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circuferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
|
Función |
Abreviatura |
Equivalencias (en radianes) |
|---|---|---|
|
sin (sen) |
|
|
|
cos |
|
|
|
tan |
|
|
|
ctg (cot) |
|
|
|
sec |
|
|
|
csc (cosec) |
|
Con carácter general un cambio que resulta muchas veces útil expresar las potencias funciones trigonométricas mediante funciones de ángulos múltiples, eso puede lograrse gracias a las siguientes identidades:
Por ejemplo las dos fórmulas anteriores permiten substituir potencias complejas de la función coseno por el coseno de ángulos múltiplo:
Integral que contiene potencias de senos y cosenos 
-
- En general, se intenta escribir un integrando en el que intervienen potencias de seno y coseno en una forma donde se tiene sólo un factor seno (y el resto de la expresión en términos de coseno) o sólo un factor coseno (y el resto de la expresión en términos de seno).
- La identidad
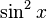



 permite convertir de una parte a otra entre potencias pares de seno y coseno.
permite convertir de una parte a otra entre potencias pares de seno y coseno.
- Existen 3 casos:
Cuando n es impar
Cuando  , podemos apartar un factor del seno y sustituirlo por la identidad
, podemos apartar un factor del seno y sustituirlo por la identidad 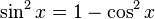 para poder expresar los factores restantes en términos del coseno:
para poder expresar los factores restantes en términos del coseno:
Al tener el integral de esta forma se puede resolver por medio de sustitución haciendo  ,
, 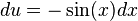 . Como en la expresión no tenemos un
. Como en la expresión no tenemos un 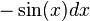 multiplicamos ambos lados por
multiplicamos ambos lados por  y nos queda la expresión
y nos queda la expresión  que ya podemos sustituir:
que ya podemos sustituir:
Cuando m es impar
Cuando  , podemos de la misma manera apartar un factor de coseno y emplear
, podemos de la misma manera apartar un factor de coseno y emplear  para poder expresar los factores restantes en términos del
para poder expresar los factores restantes en términos del  :
:
al hacer  y
y 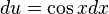 tendríamos
tendríamos
Cuando m y n son pares
Cuando dichas potencias son pares a la vez  y
y  , podemos aplicar las identidades de la mitad de ángulo:
, podemos aplicar las identidades de la mitad de ángulo:
algunas veces es útil usar la identidad:
sería igual a:
Ejemplo #1
- Solución Lo primero que tenemos que ver es que la potencia impar la tiene la función seno, esto nos hace notar que estamos en el primer caso que describimos arriba, entonces aplicamos el algoritmo,
Sustituyendo 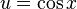 , tenemos
, tenemos  luego:
luego:
Integrales que contiene potencias de tangentes y secantes 
-
Se puede usar una estrategia similar a la anterior.
- Puesto que:
-
 , se puede separar un factor
, se puede separar un factor 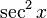 y convertir la potencia restante (par) de la secante en una expresión relacionada con la tangente por medio de la identidad
y convertir la potencia restante (par) de la secante en una expresión relacionada con la tangente por medio de la identidad  .
.
-
- O bien, puesto que:
-
 , se puede separar un factor
, se puede separar un factor  y convertir la potencia restante (par) de tangente a secante.
y convertir la potencia restante (par) de tangente a secante.
-
- Existen 3 casos:
Cuando n es par
 separar un factor de
separar un factor de 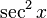 y utilice
y utilice  para lograr expresar los factores restantes en términos de
para lograr expresar los factores restantes en términos de 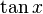 :
:
de esta manera podemos hacer  y
y  y el integral quedaría así:
y el integral quedaría así:
Cuando m es impar
 apartar un factor de
apartar un factor de  y emplear
y emplear  para poder expresar los factores que restan en términos de
para poder expresar los factores que restan en términos de  :
:
de esta manera se puede hacer  y
y  , con lo que queda
, con lo que queda
La tangente tiene potencia par 
La Secante tiene potencia impar
En este caso se procede a integrar por partes.
Ninguno de los anteriores
Al no encontrar la forma de ninguno de los pasos anteriores, se traslada a  y
y  , recordando que:
, recordando que:
Para otros casos, las directrices no son tan claras. Podría ser necesario usar identidades, integración por partes y, ocasionalmente, un poco de inventiva.
-
- A veces será necesario poder integrar
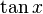 por medio de la fórmula establecida:
por medio de la fórmula establecida:
- A veces será necesario poder integrar
-
- Se necesitará también la integral indefinida de la secante:
Esta última se podría comprobar mediante la derivación de lado derecho, o como sigue:
- Primero se mutiplican numerador y denominador por
 :
:
- Si se sustituye
 , después
, después  , también, la integral se convierte en:
, también, la integral se convierte en:
- Así, se tiene:
- NOTA: Para integrales que contienen cosecantes y cotangentes, la estrategia es análoga a la del par secantes-tangentes. Recordar la identidad:

Reducción a funciones racionales
Si el integrando puede expresar como una función racional de funciones trigonométicas:
(*)
Entonces el cambio:
permite reescribir la integral como:
Que resulta ser una función racional, y por tanto, de integración mecánica.

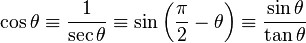

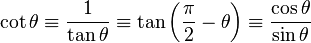














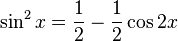
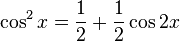



![\int [\frac{1}{2} + \frac{1}{2}\cos 2x]^{p}\; [\frac{1}{2} - \frac{1}{2}\cos 2x]^{k} dx](http://upload.wikimedia.org/math/f/8/a/f8ad147bc91a1a82fa5309934f92f7e2.png)






![\int [1 + \tan^{2}x]^{k-1}\;\tan^{m}x\;\sec^{2}xdx](http://upload.wikimedia.org/math/0/c/d/0cd003af7e7d615137156117e129d5e9.png)
![\int [1 + u^{2}]^{k -1}\;u^mdu](http://upload.wikimedia.org/math/e/3/e/e3e2074f101e0aecf783fb20fc3fc5a4.png)













![\int R(\sin(x),\cos(x))\ dx, \qquad R(x,y)=\frac{P(x,y)}{Q(x,y)},\ P,Q\in \R[x,y]](http://upload.wikimedia.org/math/e/d/6/ed6d5e1e01fdce9440f3cb04afe21163.png)

